昨天講完了zk-SNARKs為什麼那麼常運用在區塊鏈的原因,還沒看過的可以點這邊觀看,那麼今天就來說明一下zk-SNARKs的流程,回想一下之前在這篇文章所提到的非交互式零知識證明,裡面用了一個比喻,說到如果一個證明者想要證明自己擁有某把公開的公鑰所對應到的私鑰,就要對一個由許多驗證者創造出來的一個隱藏亂數做簽名,基本上這樣就可以完成非交互式零知識證明,可是問題來了,我們要怎麼對一個我不知道的東西做簽章呢?即使真的做出來,驗證者要怎麼驗證這個的真偽呢?而且這只是一個身分認證的命題,萬一不是這個命題,證明方式是否要重新設計?基本上看完我之前講的非交互式零知識證明應該都會產生種種疑問,而要回答這些問題就需要理解這背後深奧的數學,秉持著淺談的原則,我希望能用比喻的方式讓你們稍微理解非交互式零知識證明的面貌,我就從zk-SNARKs的流程來帶大家一步一步解析。
在zk-SNARKs開始之前,會有個可信設置的動作,還記得我之前說過非交互式零知識證明需要讓很多驗證者參與出題嗎?這便是可信設置在做的動作,每個人都可以把自己選的亂數透過同態隱藏的方式丟進去,假如你不信任其他驗證者,你也可以自己丟亂數進去,而經過這個可信設置後,會有一個叫做「Power of Tau」的東西產生,這個Power of Tau是什麼呢?我們大家都會丟一個亂數結合形成一個大亂數嘛,這個大亂數與他的"多次好夥伴們"經過同態隱藏函數出來的結果便是Power of Tau,舉個例子,假設現在的大亂數叫做,且使用的同態隱藏函數叫做
,那麼Power of Tau便是
、
、
、
、...、
,為什麼需要他的多次呢?我們來想一下,我們知道這個
之後會做為輸入帶入我們要解的題目中,然而現實情況我們不會直接看到
,而是他同態隱藏後的結果,然而我們要解的題目可能會有二次式、三次式等多次的情況產生,我們都知道這裡的同態隱藏只能做加法同態,如果只給
,我們是湊不出
的,因此我們會希望在可信設置的時候,就把這些東西給提供出來,方便之後帶入問題的數學式,並且能用同態隱藏的方式進行驗證。
接下來就開始進入zk-SNARKs三大演算法了,這三大演算法基本上都是給輸入,然後吐輸出的東西,而最一剛開始要做的是G演算法。G演算法要給的輸入是什麼呢?他主要需要給你要做零知識證明的「命題」以及可信設置產出來的「Power of Tau」,而這邊的命題是需要經過轉換的,我們要先將命題轉換為數學式,基本上任何命題都必須轉成數學式才能當作輸入丟進來,所以所有符合零知識證明的命題都可以做zk-SNARKs,而這個命題跟Power of Tau丟入後便會產生出證明鑰匙(proving key)跟驗證鑰匙(verification key)這兩把鑰匙是什麼呢?我做個比喻好了,假設我們對一個亂數丟進一個同態隱藏的函數中,就像是我們將一封信塞入信封中,而我們現在拿到這個信封要對裡面的信件做簽名,顯然是辦不到的,就算簽名完,驗證者拿到這個信封也沒辦法檢查裡面的簽名,但是假設我們在一剛開始就給出一個可以穿透信封的墨水以及一個可以穿透信封的手電筒會發生什麼事情?這樣要簽名的人便可以拿著特殊的墨水進行簽名,而要驗證的人可以拿著手電筒檢查信封裡面的簽名,因此,這瓶墨水便是證明鑰匙,相對的,這個手電筒便是驗證鑰匙。
G演算法可以說是zk-SNARKs的起點,當證明者找到他想證明的命題後,會使用G演算法產出對應的證明鑰匙與驗證鑰匙並將他們跟著命題與命題中的公開資料全都公開,如果以身分驗證來說,這邊的命題會是一個私鑰生成函數,而公開資料會是該把公鑰,緊接著他便會做P演算法。
證明者在拿到證明鑰匙後,可以將自己的私有資料以及檯面上公開的命題、公開資料與證明鑰匙帶入P演算法,P演算法會利用這些嘗試算出證明(proof),而這個證明便是之後要驗證的關鍵,而通常你命題轉換後的數學式愈難,要算出證明的時間便會愈久,而當算出證明過後,證明便可以公開出來交給驗證者讓他們執行V演算法進行驗證。
一旦當該公開的資料都公開出來了,驗證者就可以將檯面上所有公開資料進行V演算法驗證,V演算法要帶入的是命題、命題對應的公開資料、驗證鑰匙以及證明者提供的證明,V演算法的輸出就只有通過與不通過兩種,只要結果是通過,就代表證明者提出的證明是正確的,證明者便能通過這次的零知識證明。
好了,介紹完zk-SNARKs的三個演算法之後,是不是有點小混亂,不過沒關係,我幫你們整理了一下,畫成下面的圖片: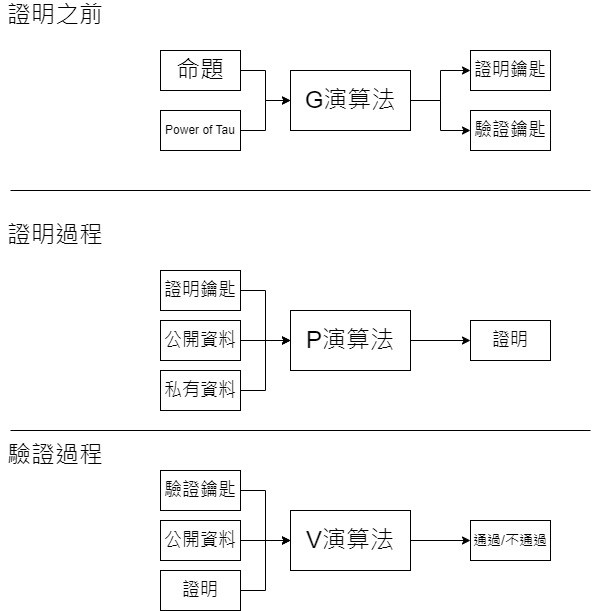
通常在區塊鏈上的應用都是證明者將要驗證的命題透過zk-SNARKs產出驗證鑰匙後,寫一個帶有驗證鑰匙的驗證程式,放到區塊鏈上,之後只要將公開資料以及證明當作輸入帶入之後,只要能通過,就代表零知識證明成功,區塊鏈上每一個礦工皆為驗證者,驗證著整個零知識證明。假如果我們把整個zk-SNARKs簡化,可以發現整個流程基本上就是證明者透過丟出公開資料與證明,來去證明自己真正擁有私有資料,所以整個零知識證明的過程,可以想像出是在加密私有資料變成證明,且透過證明我能驗證私有資料的合法性,記住這點後,基本上就可以拿它來做許多應用了,而在做應用之前,應該先了解一下,我們有哪些工具可以幫助我們做應用,那麼我明天就來談談那些能幫我們開發zk-SNARKs的工具。
